どの程度の微細化が必要か知るため、筆者が昔勉強した内容をひっくり返して見ると、ありました、Hall-Petchの法則! 当時は、ふう〜ん 程度の印象だったと思いますが、いざ必要に応じて見直して見るとなんとも興味深い!やはり、一方的に詰め込まれても頭に残りませんが、自ら求めれば自ずと知識欲が湧いて来てつき詰めようとする。「必要は発明の母」とは良く言ったものです。
Hall-Petch則
一般に,材料の降伏強度 と平均結晶粒径 d の間には,次式の関係が経験的に成り立つことが知られています。
$$\sigma_y=\sigma_0+\frac{k}{\sqrt{d}}$$
ここで,$$\sigma_y$$ は降伏応力,$$\sigma_0$$ は摩擦応力,k は結晶粒界のすべりに対する抵抗を示す定数。
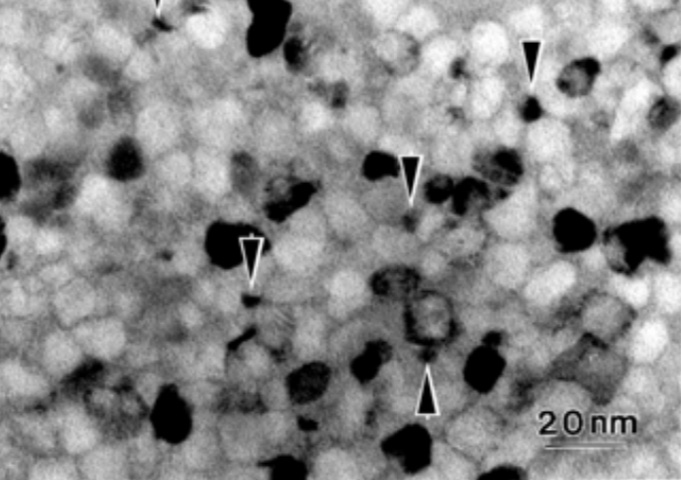
では、実在に式に当て嵌めてみましょう。残念ながら、ルナチタニウムは現時点実在していませんので、現在最も一般的且つ航空機にも大量に採用されているTi-6Al-4V合金の式を参考にしました。この式に当て嵌めてみると、4.5GPaの強度を出すためには、平均粒径約15nm(ナノメートル)にする必要があります。
15nmって言われても実感が湧かないと言う方もいるでしょう。1nmとは、1/1000000mm(100万分の1mm)になります。物凄くザックリ比較すると、粒径10nmの粒子を1円硬貨の大きさ(20mm)に拡大した場合、同じ倍率で身長170cmの人間を拡大すると、だいたい日本列島と同じ長さの身長になります。やっぱり解りにくいですね。
筆者が日頃扱っているチタン合金の結晶粒度は、小さくてもせいぜい15μm(マイクロメートル)ですので、nmに直すと15000nm。ここから未だ1/1000にしないといけません。そんな方法があるのでしょうか?